题解 P4085 【[USACO17DEC]Haybale Feast】

发表于 | 更新于

线段树、树状数组、ST表、分块、堆……等数据结构，但是复杂度都至少是$nlogn$的，于是我写了个尺取法+单调队列的方法，时间复杂度$O(n)$

单调队列维护区间中$si$~$sj$的最大值,这里运用到了一点贪心策略，如果两个区间有包含关系，那么大的区间最大值一定$\geqslant$小的区间最大值，所以对于每一个$i$，我们去前面找第一个$head$，使$sum_{i,j}\geqslant m$

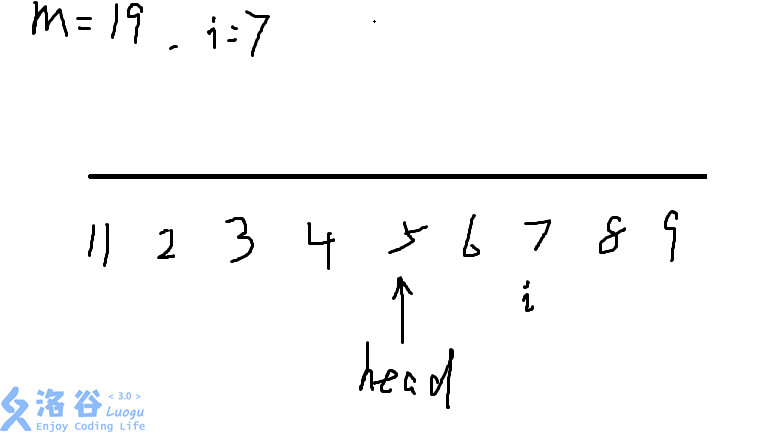
如图所示，我们选择$5$作为$head$而不是前面的$11$、$2$、$3$、$4$，是因为区间更长，就像在一个数列中加入了另一些数，另一些数中可能有大于原数列的最大值，因为要求最大值的最小值，故不是最优。

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
#include <bits/stdc++.h>
#define ll long long
using namespace std;
inline int read(){
   int s=0,w=1;
   char ch=getchar();
   while(ch<'0'||ch>'9'){if(ch=='-')w=-1;ch=getchar();}
   while(ch>='0'&&ch<='9') s=s*10+ch-'0',ch=getchar();
   return s*w;
}//快读
int a[300000],b[300000],p[300000],head=1,head1=1,tail1=0,ans=2100000000;
ll sum,m;
inline ll Min(int a,int b){
    if (a>b)return b;
    else return a;
}
int main(){
    int n=read();
    scanf("%lld",&m);
    for (int i=1;i<=n;i++) a[i]=read(),b[i]=read();
    for (int i=1;i<=n;i++){
        sum+=a[i];
        while (head<=i&&sum-a[head]>=m){
            sum-=a[head];head++;//这里注意要先减再head++，尺取法与单调队列在这里都容易出错
        }
        while (head1<=tail1&&p[head1]<head) head1++;//若队首位置小于区间左端，则出队
        while (head1<=tail1&&b[i]>=b[p[tail1]]) tail1--;//若新加入的数大于队尾，则队尾出队
        p[++tail1]=i;//放入队列
        if (sum>=m)ans=Min(ans,b[p[head1]]);
        }
    printf("%lld",ans);
}